Transformées de Fourier La petite histoire Comprendre simplement Domaines de présence Son interprétation dans l'avenir Les références Mais encore …

by Pepe ©   Accueil  Arborescence  Page précédente

La petite histoire  Up Page Origine, raisons, hasard

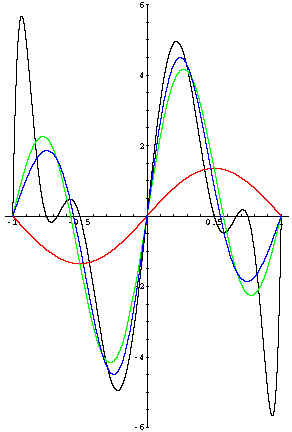
Comprendre simplement  Up Page Vulgarisation, de 7 à 77 ans Une transformée de Fourier est une transformation mathématique qui permet de trouver toutes les fréquences constitutives d'un signal (on parle aussi de décomposition spectrale d'un signal). 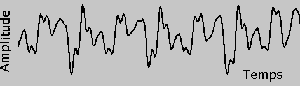  Le signal ci-contre, dont la forme peut paraître à première vue très compliquée peut en fait, via transformées de Fourrier, être représenté comme la superposition de signaux sinusoïdaux simples.     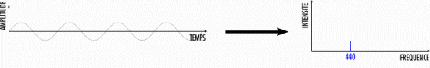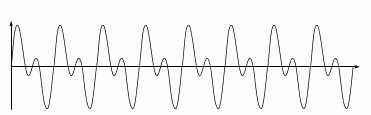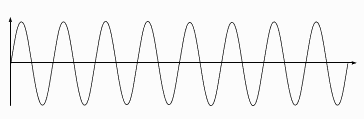Pour mieux fixer les idées, voici la représentation d'un signal très simple : le La 440 (ou la du diapason) Ce signal vibre 440 fois par seconde: sa fréquence est de 440 hertz (ou Hz) A gauche: sa représentation amplitude-temps A droite: sa représentation intensité-fréquence (ce qu'on appelle le spectre)   Considérons maintenant, ce signal (relativement simple): Il peut-être décomposé sous la forme des deux signaux suivants: 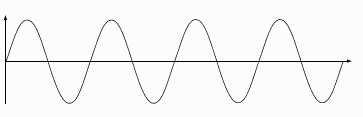+ En terme de spectre (voir ci-dessous), on voit que le signal général est la superposition d'un signal qui vibre à 440 Hz et d'un signal à 880 Hz, les deux pics de fréquences ayant ici la même intensité.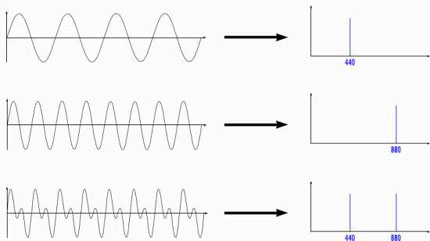

Domaines de présence  Up Page Monde présent

Son interprétation dans l'avenir  Up Page Monde futur

Les références  Up Page Réseau Pepe Automates Intelligents   Pourquoi ce site Je crois que, si les êtres humains que nous sommes ne parviennent pas toujours à évoluer comme ils le souhaiteraient _à s'épanouir professionnellement, sentimentalement et sexuellement (ce que j'appelle les "trois pôles d'intérêts", en psychologie)_ c'est parce qu'il y a des barrages qui entravent leur désir d'accéder à un rêve inachevé. Je pars du principe que tout est possible, à condition de s'entourer de gens qui nous poussent à croire en nous.   Contribuer au Réseau Pepe Ce site est avant tout une encyclopédie ouverte à l'imagination et au savoir, où chacun(e) d'entre vous peut participer. Si vous avez envie de partager une passion, ou si vous sentez le besoin de vous exprimer sur un point précis, je vous invite à m'adresser un e-mail (adresse électronique accessible sur ma page d'accueil).

Mais encore …  Up Page Ce que vous avez toujours voulu savoir